3D Computer Vision 관련 자료는 Minnesota 대학교 박현수 교수님의 CSCI 5563
자료를 사용하였습니다.
https://www-users.cse.umn.edu/~hspark/csci5563_S2021/csci5563.html
https://www-users.cse.umn.edu/~hspark/csci5563_S2021/csci5563.html
Slide Lecture Readings Introduction Camera Model Ch 6 Projection Matrix Ch 6 Projective Lines Ch 8 Criminisi et al., Single View Metrology, IJCV, 2000 Camera Localization via Vanishing Points Ch 8 Image Transformation Ch 2 Linear Estimation Appendix 4, 5 S
www-users.cse.umn.edu
지난 글에서 카메라 촬영시 실제 3D 좌표에서 2D 좌표로 투영되는 과정에 대해서 설명을 드렸습니다.
이번 시간에는 카메라를 여러대 사용했을때 기준이 되어주는 월드 좌표계와 월드 좌표계를 도입하였을때의 투영과정, 투영되는 과정을 행렬로 표현한 투영 행렬(Projection Matrix 혹은 Camera Matrix 라고도 부릅니다.)에 대해서 알아보도록 하겠습니다.

우선 지난글에서 설명드린 카메라 내부파라미터 $K$에 대해서 다시 간단하게 보고 시작하도록 하겠습니다.
카메라 내부파리미터 $K$는 3D 좌표 $(X, Y, Z)$를 픽셀 좌표계의 한점 $(u, v, 1)$로 투영시켜주는 행렬입니다.
그림 1. 에서 처럼 실제 3D좌표 $(X, Y, Z)$에 곱해져서 픽셀 좌표계의 한점 $(u, v, 1)$ 좌표를 계산할 수 있습니다.

3차원의 좌표는 따로 기준이 되는 원점이 존재하지 않기 때문에 촬영을한 카메라가 바라보고 있는 방향을 기준으로 하여(카메라가 바라보는 방향 Z축, 카메라 오른쪽 X축, 카메라 아래 Y축) 촬영된 복도 타일의 한점을 임의로 원점으로 지정할 수 있습니다.

하지만 만약에 카메라 여러대가 다른방향에서 복도를 촬용하였을때 타일의 같은 한 점을 원점으로 설정했다면 첫번째 카메라 기준 원점 $X_{C1}$, 두번째 카메라 기준 원점 $X_{C2}$ 등 여러 카메라 기준에서의 원점들이 존재하게 됩니다. 이런 경우 어떤점을 원점으로 고려하는게 맞는것일까요?

위에 설명한 것과 같이 어느 카메라를 기준으로 잡는지에 따라 원점의 좌표가 달라지기 때문에 여러 기준을 하나로 통합하여 표현할 수 있는 새로운 기준이 필요합니다.
이러한 문제를 해결하기 위해 새로운 3차원 좌표계를 도입하게 되었는데 이를 월드 좌표계(World Coordinates) 라고 합니다.
월드 좌표계는 하나의 기준이 되는 새로운 좌표계로써 여러 카메라들이 존재하더라도 각 카메라들의 좌표계들을 하나의 월드 좌표계로 변환하여 표현함으로써 카메라들 간의 상관 관계를 보다 쉽게 표현할 수 있게 하는 역할을 하게 됩니다.
새로운 월드 좌표계를 도입함으로써 기존 투영되는 과정에도 변화가 생겼습니다. 기존에는 카메라 좌표계 하나만을 기준으로 하여 투영되는 과정을 계산을 했다면 이제 월드 좌표계가 도입이 되면서 좌표계간의 변환까지 고려한 투영과정을 계산해야 합니다.
좌표계간의 변환 과정을 알아보기 위해 우선 좌표계 축의 회전에 대해서 먼저 알아보도록 하겠습니다.

축의 회전을 알아 보기전에 우선 점의 회전에 대해 먼저 알아보도록 하겠습니다. 점의 회전이란 원점을 기준으로 하여 각도의 변화에 따라 이동하는 것을 의미합니다. $X$의 점이 원점을 기준으로 $X_{1}$점으로 회전하게 되었을 때 두개의 점에대한 회전 행렬은 위 그림과 같습니다.

이번에는 축만 회전했을 때의 회전행렬이 어떻게 나오는지 알아보도록 하겠습니다.

회전하기 전 기준이 되는 축을 World축, World 축을 $\theta$만큼 회전한 축을 Camera축, 점 $X$는 (1,1) 이라고 가정을 하고 설명드리겠습니다.
1) World축에서 축과 점이 같이 $\theta$ 만큼 회전하게 되면 World축 기준 점 (1,1)은 Camera축 기준 (1,1) 지점(파란색)에 점이 위치하게 됩니다.
2) World축에서 축만 $\theta$ 만큼 회전하고 World축 기준 점(1,1)은 Camera축을 기준으로 빨간색 지점에 점이 위치하게 됩니다.
3) 점은 회전하지 않고 축만 회전하게 되면 Camera 축 기준 (1,1)좌표를 -방향으로 $\theta$ 만큼 회전한 결과를 얻게 된다는 것을 확인할 수 있습니다. (보라색 화살표)
결론적으로 축만 $\theta$만큼 회전시키게 되면 점은 -$\theta$ 방향으로 회전한다는 것을 알 수 있습니다.

따라서 축을 회전시키는 행렬은 $sin\theta$의 부호가 반대로 된 행렬이 되게 됩니다.



정리해 보자면 좌표계 축의 변환 과정에서 회전만 고려하게 되면 다음과 같은 과정을 통해 투영과정을 계산하게 됩니다.
1) 월드 좌표계 좌표 $(X, Y, Z)$에 카메라 좌표계로 변환시켜주는 회전 행렬 $R_{w}$을 곱하여 카메라 좌표계 좌표$(X_{c}, Y_{c}, Z_{c})$로 변환
2) 카메라 좌표계 좌표$(X_{c}, Y_{c}, Z_{c})$에 카메라 내부 파라미터 K 행렬을 곱해줌으로써 픽셀 좌표계 $(u, v, 1)$로 투영
지금까지 회전만 있을 경우에 대해서 알아보았습니다.
실제 환경에서는 좌표계의 회전뿐만 아니라 이동까지 포함하여 고려를 해야하기 때문에 회전과 이동을 고려했을때를 알아보도록 하겠습니다.


이전에 설명드린 것 처럼 회전만 고려했을 경우 그림 13. 처럼 회전행렬을 얻을 수 있게 됩니다.

카메라 좌표계의 좌표축과 월드 좌표계의 좌표축간의 이동까지 변환이 필요한 경우를 그림 14. 의 좌표축 그림과 같이 표현하였습니다.

좌표축의 이동은 점의 이동과 마찬가지로 x의 방향으로 이동량 $t_{x}$, y의 방향으로 이동량 $t_{y}$를 더해준 것으로 나타낼 수 있습니다.
우선 회전행렬을 통해 우선 좌표축을 회전 시킨 후 그 다음 이동량 $t_{x}$, $t_{y}$를 더해주게 됩니다.

회전 후 이동하는 계산을 식으로 정리하여 나타내게 되면 $X_{C} = R_{W}X + t$ 로 나타낼 수 있습니다.
여기서 식을 간단히 하기 위해 R_{W}로 묶어 식을 표현하게 되면 $X_{C} = R_{W}(X - C)$ 로도 나타낼 수 있습니다.
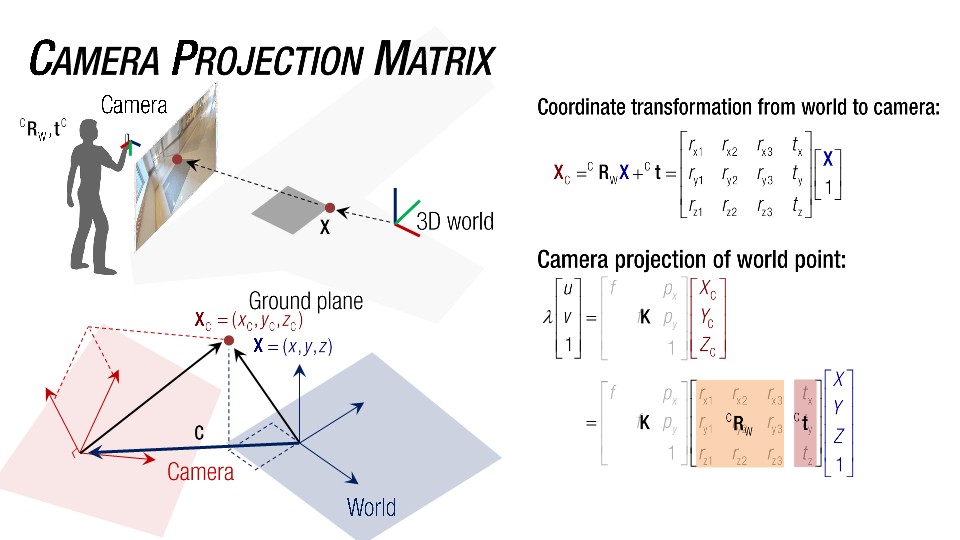
좌표계간의 변환을 고려하여 카메라로 물체를 촬영했을때 투영되는 전체과정을 다시 정리해 보도록 하겠습니다.
($X$ : 월드 좌표 , $X_{C}$ : 카메라 좌표, $X_{P}$ : 픽셀좌표)
1) 월드 좌표계 에서 카메라 좌표계 로 변환하는 행렬을 곱하여 좌표계간 변화를 시킨다. $X \rightarrow X_{C}$
2) 변환된 좌표 에 카메라 내부 파라미터인 $K$ 행렬을 곱하여 픽셀좌표계로 투영시킨다. $X_{C} \rightarrow X_{P}$

픽셀 좌표계에서 다시 월드 좌표계로 역변환 과정을 식으로 정리하게되면 그림 18. 처럼 나타낼 수 있습니다.
여기서 $\lambda(KR_{W})^{-1}$는 그림 18.에서 보이는 것처럼 점선화살표의 방향을 나타내게 되고 $C$는 점선화살표의 원점을 나타내게 됩니다.

종합해서 정리해 보면
카메라 센서와 핀홀간의 공간적 관계를 변환시켜주는 K 행렬을 카메라의 내부 파라미터,
카메라의 좌표축과 월드 공간의 좌표축 간의 관계를 변환시켜주는 $[R | t]$ 행렬을 카메라 외부 파라미터,
$K$ 행렬과 $[R|t]$ 행렬을 합쳐서 카메라 행렬(Camera Matrix) 또는 투영 행렬(Projection Matrix)라고 부릅니다.
실제 환경에서 카메라로 물체를 촬영했을때 고려해야할 사항이 하나 더 존재하게 되는데
그것은 바로 카메라의 렌즈에 의해 발생하는 왜곡 입니다.
카메라 렌즈의 왜곡에 대해서 간략하게 설명하고 이번 글을 마치도록 하겠습니다.

그림 20. 에서 보이는 것 처럼 바닥 타일을 기준으로 일직선으로 점선을 그렸을때 왜곡이 없는 이상적인 환경의 경우 타일과 점선이 일치해야 하지만 보시면 영상의 테두리 쪽으로 갈수록 점점 점선과 타일간의 간격이 벌어지는 것을 볼 수 있습니다.
일반적으로 렌즈의 경우 렌즈의 테두리에서 가장 많이 빛이 굴절되게 되고 가운데로 갈수록 굴절이 일어나지 않아서 영상의 가장자리 부분으로 갈수록 왜곡이 심해지게 됩니다.

본 강의자료에서는 카메라 왜곡을 가장 쉬운 방법의 모델로 설정하여 왜곡이 발생했을 경우를 모델링 하였습니다.

그림 22.식으로 모델링 하여 왜곡을 없앨 경우 다음과 같은 결과 사진을 얻을 수 있게 됩니다.
지금까지 까지 월드 좌표계와 월드 좌표계를 도입하였을때의 투영과정, 투영되는 과정을 행렬로 표현한 투영 행렬(Projection Matrix 혹은 Camera Matrix 라고도 부릅니다.), 정말 간략하게 카메라 왜곡에 대해서 알아보았습니다.
다음 글에서는 Projective Line이 무엇인지에 대해서 설명드리도록 하겠습니다.

'3D Vision 공부' 카테고리의 다른 글
| [CSCI 5563] 3. Projective Line (0) | 2021.11.04 |
|---|---|
| [CSCI 5563] 1. 3D Point Projection (4) | 2021.10.12 |

